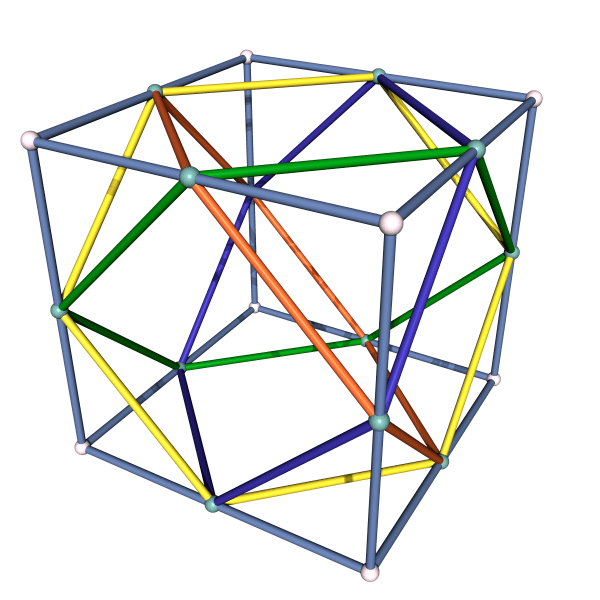In Óskar Jónasson’s film Reykjavik-Rotterdam, a painting by Jackson Pollock plays a marginal but hilarious role.
The pictures in this post are inspired by drip-art and action painting.
They are not quite up to Pollock’s standard, but I must say I like them.
Of course they are not paintings, but landscape closeups taken off the coast of Westman Islands.
The artist? Hard to say, but at least partially responsible are the doves.
A torus is obtained by rotating a circle around a axis in the same plane. As such, it has two families of circles on it: the ones coming from the generating circle, and the orbits of the rotation. This allows you to slice the torus open using vertical or horizontal cuts, with the cross sections being perfectly round circles,
Of course, when you do this to your bagel, you do not really expect circles. But neither would you expect the bagel to be hollow.
The surprise, however, is that there is yet another way to slice a torus, still with perfectly circular cross sections. These are the Villarceau circles.
Here is how to do it. Looking at a vertical cross section, cut along a plane that’s perpendicular to your cross section and touches the two circles just above and below. The deeper reason for their existence lies in the Hopf fibration of the 3-dimensional sphere; these curves are stereographic images of Hopf circles.
Even more surprising is that there are certain cyclides that have six circle families on them.
A long time ago, we have looked at Soddy’s Hexlet, where a chain of six spheres is interlinked with a chain of three spheres.
There are variations of this. For instance, you can have two interlinked chains of four spheres each.
The alert visitor will have noticed that I am only displaying halves of spheres. This is because it is easier to add the other halves on one’s mind instead of thinking them away in order to see what’s behind.
There is more. If you take a suitable chain of five spheres, you can fit 10 around and through, but you will need to make three turns until the chain closes. This means that the spheres will touch their immediate successors, but intersect the ones after one and two turns, respectively.
There still is more, of course, which we leave to the reader to explore. Finding these chains is not difficult, provided you do this in the 3-dimensional sphere, and place the spheres inside complementary tori with suitable radii.
There are more things to see and do at the Museum Island Hombroich than to visit the pavilions. Artists in residence produce landscape art, and concerts are given.
I wonder how this sculpture has withered since I took these pictures in 1992. This one is part of a full circle of such outcroppings.
Mechanical structures clearly without purpose alternate with objects that are equally clearly of daily importance but could as well be just pieces of art.
An outdoor museum where the objects are exposed to the elements defies the usual purpose of a museum: the preservation of its artifacts.
Here at Hombroich the time has just been slowed down a bit, making it the main object to contemplate.
When the Cold War ended, a missile base near Neuss, Germany, became obsolete. The area was bought by the industrial real estate agent Karl Heinrich Müller, and turned into the Museum Island Hombroich.
Visitors are greeted appropriately by an Asian statue, holding his hand in the Karana Mudra gesture to ban evil spirits.
Meticulously landscaped by Bernhard Korte, the area is populated with small buildings (landscape chapels),
by Erwin Heerich that contain Asian or contemporary art, or just empty space.
Soft glass roofs and narrow doors create a balance between diffuse and directed light.
The geometric harshness of the buildings disappears in the fading light.
A cube can be sliced half so that the cross section is a regular hexagon, and this even in four different ways.
In particular, we can place regular hexagons into space so that the corners all have integer coordinates, and the hexagons face four different directions. This suggests to interlink the hexagons, for instance like so:
The mathematician immediately will ask to put as many of such linked hexagons into space, and this automatically drives the discovery of new structures or leads to connections with the already known.
In this case, it turns out that feeding one hexagon through the center of another is not so smart.
When the center spot is taken, any further hexagon through either of the first two must be placed by breaking the symmetry. Above we have threaded three hexagons through a horizontal red hexagons in a rotationally symmetric way, and placed a mirror image of this tetrad below. While these two pieces are not yet interlinked, they can together be translated as to create a very tight interlinked system of annuli (replacing the hexagons with smooth annuli).
This works in all directions, and being stuck somewhere within this tangle will look like this:
The hyperbolic plane is a geometry whose points are those of a disk, and the lines are circular arcs that meet the boundary circle of the disk at a right angle. Like so:
We see that the arcs in this figure cut out regions, and the central one looks like a deflated square. However, to the hyperbolic eyes the circles are actually straight, and all regions would be considered congruent squares. There is yet another difference to Euclidean geometry: These squares have corners with 60 degree angles, instead of the traditional 90 degrees. In fact, hyperbolic people can make squares with any angle less than 90 degrees at the corners, all the way down to 0 degrees. Then the vertices lie on the boundary of the disk, and we are getting what is called an ideal square.
Of course there is also hyperbolic space, represented by a round ball. The planes are spherical shells meeting the boundary of the ball at a right angle. We can make cubes in hyperbolic space, with dihedral angles less than the traditional 90 degrees. This time, when the cube becomes ideal (i.e. when the corners lie on the boundary of the ball), the dihedral angles of the hyperbolic cube have shrunk down to 60 degrees.
Because six such cubes will fit around an edge very much like six hyperbolic 60 degree squares fir around a corner, we are able to tile all of hyperbolic space with ideal cubes. Visualizing this is a challenge, as if we just draw all the cubes, we will just see a ball, and all the effort was in vain.
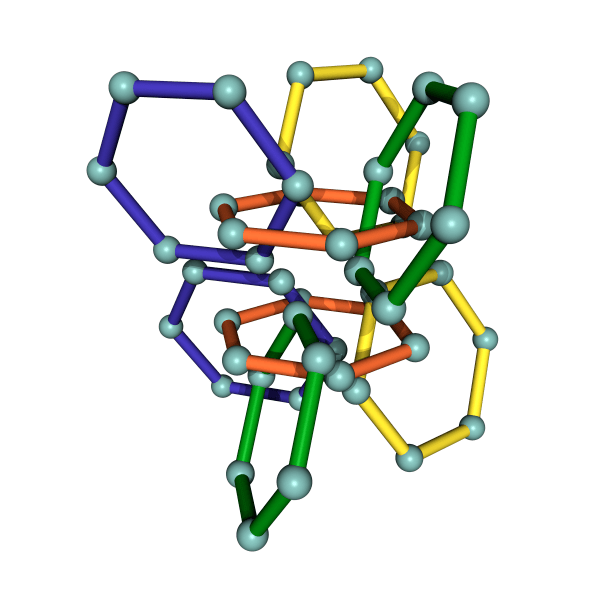
But we can leave out some of the cubes. If we start with the central ideal cube, and just take those cubes that can be obtained by rotating about the edges by 180 degrees, we get after a few steps the following object, shown as a stereo pair for cross-eyed viewing.
The final image is obtained by applying more such rotations, and making the material relective.
Lets look at circles with centers at points with integer coordinates and equal radii. When the radii are small, the circles will be disjoint. Something interesting first happens when the radius becomes 1/2, because then the circles touch.
When the radii grow, the circles will intersect, and interesting patterns emerge. These patterns change continuously,
but when a special intersection occurs, the complexity of the intersection pattern increases. The next special intersection after r=0.5 occurs at r=0.7071, when circles that are diagonally across touch, and then again at r=1.
Often, and due to the symmetry of things, whenever two of our circles touch, a second pair of circles must touch at the same point.
Then, at r=1.17851, we have true intersections of three circles at a single point (no touching!).
Mathematicians find this interesting because the special intersections (touch or triple cross) mark singular points in the space of all such circle configurations. Understanding them means understanding the whole space.
It is of course very satisfying that these singularities are also esthetically pleasing, as if they knew they are special and have dressed up for the occasion.
The summer and fall 1992 I spent my free time reading Marcel Proust’s À la recherche du temps perdu. That winter, I took the photos from this page, and revisiting them now is just one of several connections to Proust’s recherche.
Of course these were shot with film, and in black and white, appropriate for season and theme. The location is the Sieg valley near Bonn in Germany, where I happened to come across a temporarily abandoned construction site.
The time was literally frozen. Everything had been more or less orderly put ready to use.
This was a curious sight. Unless our daily business is construction, we usually do not see these things, because they are buried or covered up, in the hope that they will function even in hiding.
Not esthetics, but pure purpose is the reason for these designs. And because I did and do not know the actual purpose of them, they became for me the abstraction, the idea of purpose itself.
This tilting away from reality towards abstraction has always fascinated me, already (at least) 23 years ago.
There are essentially two very symmetric ways to tile the plane with circles. One can use the square tiling, of the more efficient hexagonal tiling.
In space, we can use the cubical tiling to generalize the square tiling, as I did in Spheres V. But one can do better. On one hand, one can put down one layer of spheres in the square tiling pattern, but shift the next layer diagonally to save space:
Or, one can put down one layer of spheres using the hexagonal pattern, and again shift the next layer so that its spheres fit snugly into the gaps left by the spheres of the first layer, like so:
I hope it surprises you like it did surprise me that these two approaches lead, in fact, to the same packing of spheres:
The mystery behind this is the geometry of the cuboctahedron, an Archimedean solid with both triangular and square faces:
Putting highly reflective dark blue spheres in such an arrangement within an off white cage cuboctahedral shell results in today’s sphere theme image:
The Inner Frame 