Tag: Schwarz P minimal surface

From Space to Plane (Five Squares I)

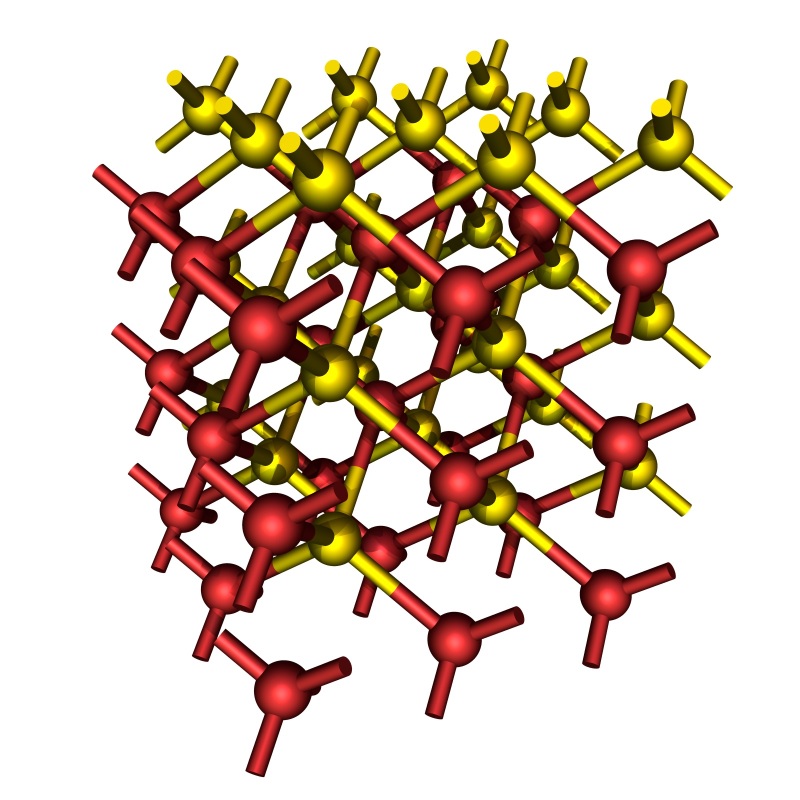
Euclid allows us to place four squares around a vertex. If we are not satisfied with that, we can either move into the hyperbolic plane, or into space. A neglected configuration is that of five squares parallel to the coordinate planes that meet at a common vertex, like so:

Pentacube3D

This is, as you convince yourself quickly, the only way to to this, up to 24 symmetric cases. The squares trace out a polygonal arc on the faces of the cube above, which we can interpret as a marking of the faces of the cube that contains the five squares. Two faces are marked by a straight segment (front and  left), three by an L-shaped segment (back, right, top), and one face is unmarked (bottom). As we did with the simple six color marking, we can centrally project the 24 cubes into the plane.

Paths

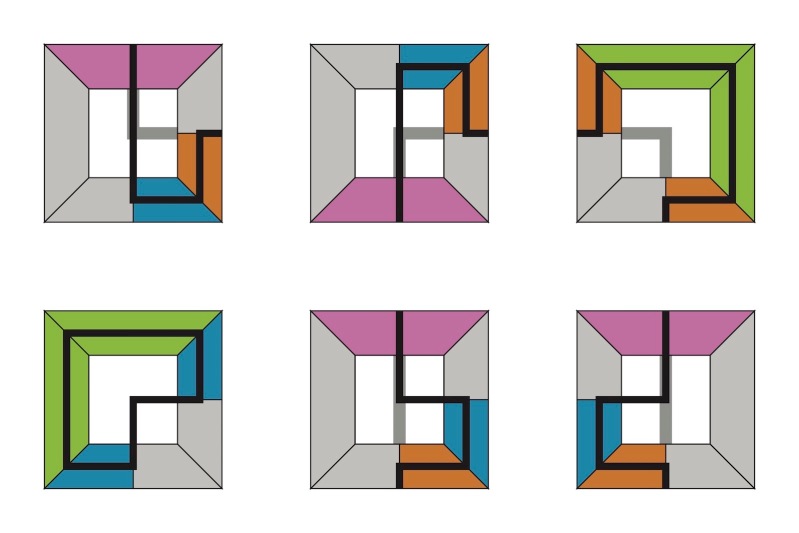
The image above shows six of these projections. The remaining ones can be obtained by 90 degree rotations. I have colored the faces of the cube to indicate what the path is doing within that face (green=go straight, blue=turn one way, orange = turn the other way, gray=don’t be there). Convince yourself that the colors suffice to reconstruct the path.

Thus we obtain a set of six tiles that allow us to explore layers of polygonal surfaces that have five squares around each vertex. For prettification, I have dropped the path and filled in the hole. No information has been lost. We are allowed to place tiles next to each other if the colors match. This is it:

Patterns

Here is a simple example of such a surface.

Schwarz

It is triply periodic and incidentally related to Schwarz P minimal surface. Two consecutive horizontal layers are represented by the two tilings below:

Schwarztile

So, we have the burning questions: Are there more polyhedra like these, do the tilings help us, and can we understand the tilings? More about it in a week or two.

Walls and Connections

The cubical lattice is a seemingly simple way to arrange spheres in space. By connecting spheres that are closest to each other, we get a line configuration I have also written about before.

c

Let’s increase the complexity by adding another copy of the same configuration, shifted by 1/2 of a unit step in all coordinate directions. This is sometimes called the body-centered cubical Bravais lattice.

CI

We can also recognize here the two skeletal graphs of the two components of the complement of the Schwarz P minimal surface. This means that the P surface will separate the yellow and the red lattices.

Now we would like to connect the two separate systems of spheres with each other. Note that each yellow sphere is surrounded by 8 red spheres (and vice vera), at the vertices of a cube centered at the yellow sphere. This suggests to connect the yellow center to just four of these red neighbors, by choosing the vertices of a tetrahedron, as to obtain a 4-valent graph. Like so:

CI2

While this is still simple, it starts to look confusing. The new skeleton has again two components, and again they can be separated by a classical minimal surface, the Diamond surface of Hermann Amandus Schwarz.

All this should remind us of the Laves graphs, which are skeletal graphs of the gyroid.

Tetra D

You can see that these skeletal graphs have girth 6. Below is a larger piece of the D-surface. Everything here is triply periodic and very symmetric. In contrast to the Laves graph, these here have no chirality.

D skeleton

Next week, we will decorate these skeletons a little.