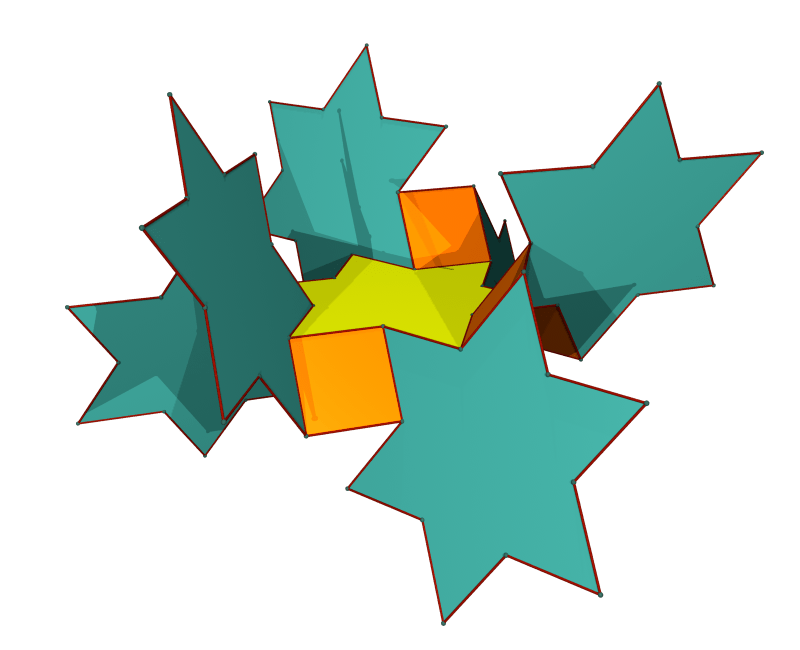
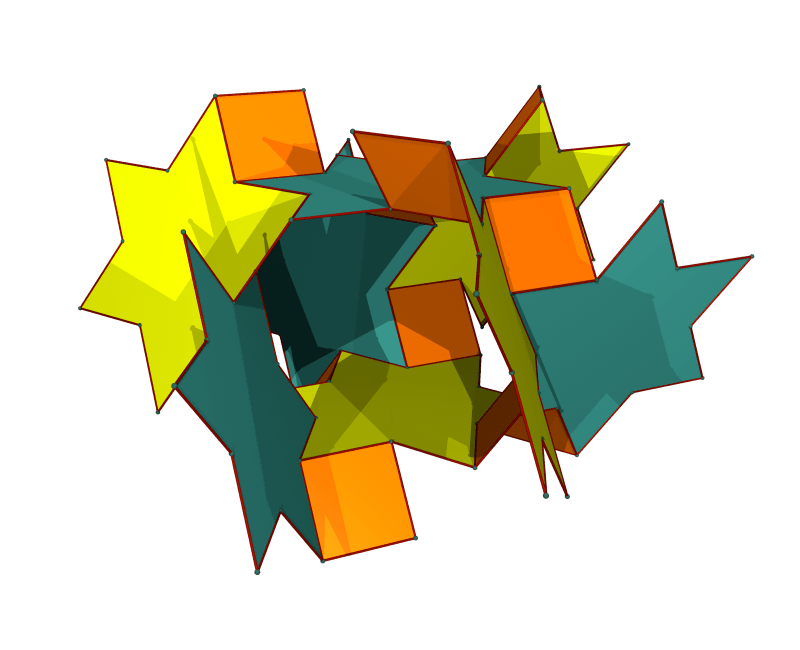After discussing trions and hexons, it’s time for the simplest variety, the quadrons. They are obtained by cutting from a square a quadrilateral that has as its vertices the square center, a vertex, and two points on the edges adjacent to the chosen vertex.

The points on the edges are chosen from the n possible points that divide the edge into n+1 equal segments. I call the number n the generation of the quadron. Above are the four generation 2 quadrons, which fit nicely into a single square, and can be regrouped to form the six square pillows I introduced a long time ago.

For generation 3, there are 9 quadrons, so they don’t fit together into squares. But we can leave one out, and try to assemble the remaining ones into two squares. There are 9 pairs of such squares, but not all quadrons can be left behind. Which ones can? The solution has to do something with the area (which color codes the quadrons above).

The 16 generation 4 quadrons fit nicely into four squares as shown above. There are 48 individual squares, which will make nice cards for another puzzle…

Then there are 75 eye-straining ways to select four of these 48 squares to obtain a complete set of generation 4 quadrons.
![]()
Higher generation quadrons become very tedious. For generation 6, there are 36 quadrons, and 2139255 many ways to fit them into a set of 9 squares.
I promised a solution for last week’s puzzle, here it is. Now you can guess the second one yourself.






















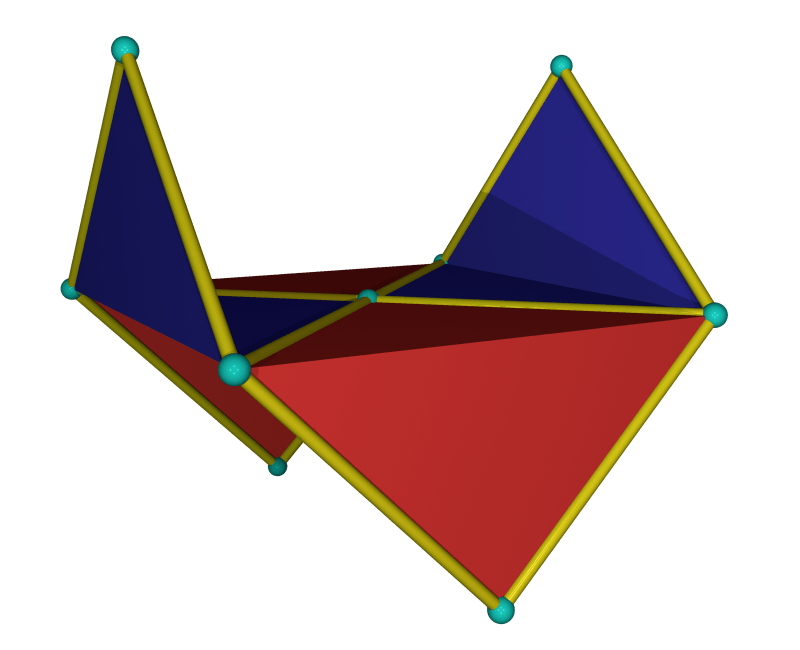
 After Alan Schoen was fired from NASA at the end of 1969, he moved back to California and continued to experiment with soap film. In October 1970, he used two identical wireframes bent into figure 8 curves consisting of two squares meeting at a vertex. When he dipped them into soapy water at a small distance from each other and pulled them out, he could poke the flat disks between the two figure 8s and create a minimal surface that looks like the top half in the picture above. It extends triply periodically to a surface of genus 5.
After Alan Schoen was fired from NASA at the end of 1969, he moved back to California and continued to experiment with soap film. In October 1970, he used two identical wireframes bent into figure 8 curves consisting of two squares meeting at a vertex. When he dipped them into soapy water at a small distance from each other and pulled them out, he could poke the flat disks between the two figure 8s and create a minimal surface that looks like the top half in the picture above. It extends triply periodically to a surface of genus 5.