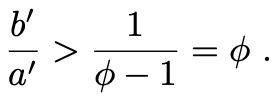The Inner Frame

Life and Death (Mogan Ridge West Trail)

A few minutes down the road from the Two Lakes Trail trailhead is another long hike, the Mogan Ridge trail. It can be done as two separate loops as a single 20 mile loop. Today I show pictures from the western portion.

Fire has devastated part of the woods. It’s a sad view, full of pain and beauty.

Death in nature is usually a slow and silent disappearance, but here the sudden death has created a togetherness of life and death with a staggering complexity.

These are sculptures — for whom, by whom?

It’s not a place to stay, but a place that will follow me.

Chomp (The Esthetics of Not Knowing)

Mathematics has a few peculiarities (inherited by their owners, the mathematicians) that irritate the uninitiated. One of them is the non-constructive aspect of many of its statements. A delicious example is the game Chomp, played with a chocolate bar. Traditionally, the top left piece is poisoned. Two players take turns selecting a piece, breaking it off together with the rectangular chunk of the pieces that are to the right or below of that piece, and instantly eating all of it. Here is an example sequence of turns. The lighter brown indicates which pieces the player is about to eat. We see that here Two has the last bite. Let’s not talk about it. Chomp 1 01

As with each move the number of uneaten chocolate pieces decreases, the game necessarily ends, and there is no draw. Mathematicians conclude from this that either One or Two has a winning strategy, i.e. a way of choosing chocolate pieces so that they win (survive), no matter what the other is doing. In Chomp, the situation is more surprising: One can always win, no matter how large the chocolate bar, but we are generally clueless how One can accomplish this. This is done by an argument that is called strategy stealing, and uses a perplexing indirect proof. So let’s assume, by contradiction, that Two has a winning strategy.

Chomp 2 01

One steals this strategy as follows: One takes the bottom right piece, and sees what Two is doing. Two will make a winning move, removing another piece and everything below and to the right. But One could have done the exact same thing, reaching the same position in the first place (as the bottom right piece will disappear with that move as well). But the nagging question remains unanswered: How does One win? What is the winning move? This happens to be a very difficult question. We not only have to consider the whole, intact chocolate bar, but also the ones that arise while chomping, and we can (very plausibly) even allow bars where some of the chocolate pieces have already been eaten (by someone) before the game even starts. For instance, below are all 132 fragmentary chocolate bars that fit in a 2×6 box where the moving player will lose, assuming the other player has their wits together.

2x6

Out of decency I have removed the poisoned piece in the top left corner, the game now simply ends when one player has no move left, meaning they lose, but keep at least their life. Below are the 182 losing positions that fit in a 3×4 box.

3x4

This is incomprehensible determinism made visible. There are patterns, though. If one encodes all possible positions that fit in a 2×10 box by a pair of binary numbers and plots the losing positions as dots in a 1024×1024 square, one gets the following:

Losers10b

Some of the patterns (like the emerging periodicity) have been partially understood, and I’ll write about that later, time and comprehension permitting.

How to Age Well

DSC 0635

The next time you worry about getting old, think twice. It could be so much worse, you could be an aging railroad, or, worse still, an abandoned aging railroad.

DSC 0641

There are plenty of those in Indiana (and I bet in your neighborhood as well), some so abandoned that they are impossible to find anymore.

DSC 0638

The CSX line that connects Bedford with Louisville has a few abandoned sidetracks where the rails have been dismantled. The photos here are from one in Orleans.

DSC 0646

While walking the remaining tracks in search for a particularly rusty railroad spike for my collection, I became increasingly fascinated by the different ways the wood of the tracks had deteriorated, in particular where the rail tie plates had been nailed into the rail ties to support the rails.

DSC 0648

Aren’t we all beautiful?

DSC 0634

Winter Walk

DSC 0356

Trail #2 in Cifty Falls State Park is one of the most rugged trails in Indiana, suitable for a harsh winter experience even without snow. It begins with a steep descent into the canyon.

DSC 0344

There we follow the creek, switching sides when needed. Occasional obstacles can easily be overcome.

DSC 0335

The canyon walls make it clear that we have little choice otherwise.

DSC 0245

What is a path anyway? Isn’t it just our choice of walking?

DSC 0329

Frozen time passes, too, and makes us hasten forward.

DSC 0214

Increasingly, the path becomes an illusion.

DSC 0256

Well, it said very rugged in the park brochure. We have been warned.

DSC 0260

While there might be no path, still there is a way.

DSC 0287

What more could we have wished for?

Whoever Hid Away (Wenckheim XI)

The last chapter of László Krasznahorkai’s last (?—?) novel Baron Wenckheim’s Homecoming provides the musically inclined reader with a very loud finale.

DSC 5628

The entire town is paralyzed in fear:

… what had been happening these past days, all of them were already living deep inside the fear that if they went outside they’d be the next to be murdered, raped, harassed, and disappeared without a single trace,…

DSC 5608

And they are wondering about the gasoline tanks and their drivers:

… but unanimously, they agreed that these drivers were waiting for something, and that’s why they didn’t get out of their trucks, they just sat behind the steering wheel, not even eating anything, they just all kept their hands on the steering wheel, as if waiting for some sign that could arrive at any moment,…

DSC 5634

As the reader expects, things get more ominous: The trucks disappear again, all animals leave the city, and knots of toads arrive from nowhere, signaling the imminent apocalypse.

… these lunatic toads had come forth from beneath the earth, as there below, in the bountiful darkness, they had all gone mad, and they had wrenched themselves out of the earth and emerged, at first they began to jump back and forth, who the hell would have thought that so many hideous toads existed beneath the earth ,…

DSC 5604

…then he took out a cigarette from the Egyptian pack, and he lit up, and in that moment, as he clicked the flame of the lighter, and he was already about to take a drag on his cigarette,… … …

DSC 5598

A town has come to its end, a book has come to its end, and, simultaneously with me finishing reading it, here an era of an eerily similar nature has come to its end, too.

Multiple Exposure (Wenckheim X)

The chapter To the Hungarians begins with newspaper editors discussing whether a certain tract they have received should be published. This tract is a hate sermon against the Hungarians, and some excerpts are read to us:

… and you’re spineless and two-faced, perfidious and contemptible, lying and rootless, because after you’ve exploited somebody, you do the same thing, namely you throw them away, you spit into their eyes, if they’re not good for anything else, because you’re primitive,…

DSC 5556

The text culminates in a generalizing damnation of all of humanity.

… moreover this true monstrosity, while he has his bad moments, at times stumbles across a good intention within himself, but he quickly forgets about that, and it remains a mere memory, but he builds upon it later, as this sort of monstrosity is convinced that fate has selected him for good, or at the very least as the representative of truth, his own truth, …

In the meantime, violence is erupting in the city, a first to statues,

unknown assailants knocked over the bust of Countess Krisztina Wenckheim, but not only that, they completely smashed apart her face with a hatchet,

then to animals,

…on Wednesday at midnight he found two cattle frozen in their own blood, their heads were also smashed apart,…

and finally to humans

…Irén’s horrific death — as they found her on the sidewalk, having to see that beloved human face now smashed into fragments…

DSC 5516

This is a chapter about fear, incited by propaganda, and backed by the actions of a nameless mob.

… she had a bad premonition about things, but what was so bad wasn’t even that people had forgotten the events of the past few days, but that the speed of all these events was like that of some kind of flood when it breaks across a dam, the events occurring and occurring one after the other,…

What we fear is not the singular incident but it becoming the daily routine. Krasznahorkai invokes this mechanism by using repeating patterns at the level of the narrative as well as that of language itself:

… because they came down Csabai Road, and they came down Dobozi Road, and they came from the Romanian border, they came from the direction of Eleki Road, from every single direction they came, rumbling, the pneumatic brakes screeching, then the engines revved, then the pneumatic brakes again, they came in a line, one after the other, and within the space of barely an hour the entire city was full of these gigantically enormous fuel carriers, and the whole thing was as if they’d ended up here by mistake, as if they wanted to go someplace completely different,…

DSC 5571

All this, the threats, the violence, the feeling of foreboding, the arrival of an enormous number of gasoline tanks, is only preparation:

… and then suddenly — as if the entire thing were dependent on a single switch — the entire city was plunged into total darkness,…

01-06-21

Turning and turning in the widening gyre

The falcon cannot hear the falconer;

DSC 9265

Things fall apart; the centre cannot hold;

Mere anarchy is loosed upon the world,

The blood-dimmed tide is loosed, and everywhere

The ceremony of innocence is drowned;

The best lack all conviction, while the worst

Are full of passionate intensity.

Memory Eternal (Wenckheim IX)

…they didn’t need any prayers, because they had their own…

Neg 2

The two images I am using today were taken in 1992 in Budapest with 35mm film, scanned at 9600 dpi (which is a silly thing), and cut apart.

Gen neg 3 95

In László Krasznahorkai’s Baron Wenckheim’s Homecoming, the chapter Losers carries out a similar dissection. We revisit most of the previous characters in separate paragraphs (in fact, sentences), which are dedicated to memory in one way or another.

Gen neg 4 90

In the time of film, the detail of a printed image was determined by many physical factors — the format of the film, its quality, its grain, the quality of the equipment, lighting conditions, magnification, and the skill of the photographer. Today, grain has been replaced by noise, which has a different character, but the problem remains the same: outrageous enlargement will result in artifacts.

Gen neg 5 80

He was out by the train stop at Bicere and trying to dissect what he was seeing down to the minutest elements,
because while he thought the bikers’ suspicions were exaggerated, he still couldn’t completely let the matter rest, because that’s how he was — …

Does this frighten us? I think so, as the megapixel wars between smartphone makers indicate. We believe to be safer with more megapixels.

Gen neg 7 60

… this matter, then, had no meaning, cause, or goal, and this in fact might have been the essence of that matter, if words themselves hadn’t given up the ghost in the mind of an eyewitness (one, moreover, not even present at the scene), because words would have come to a dead halt in this brain, …

Is it the fear that our reality itself is like this, too, that if we look too closely, it will dissolve?

Gen neg 7 40

The people who met the Baron now want to forget him. The city photographer gets busy in an unusual way:

… for the naive ones, I just delete the pictures they want me to, the pics from the train station or the entertainment events, I do it in front of them, I look for the memory card, put in the camera, and together we look for the pictures they want me to erase, and I delete the pictures in front of them; then they ask me, and I tell them that no one will ever see these pictures again, well of course, no one ever will see them, never again, rest assured, and this is all so much work that I can’t keep up with it …

I think this is what Krasznahorkai tries to accomplish in his books: slowing down time and thus expanding the monologues of his protagonists, while they are desperately trying to remain themselves.

Reporters and politicians deny that certain events have happened:

…and now he was volunteering to completely erase the speeches in question from the offices’ computers and destroy every such trace of any one of these speeches…

Gen neg 4 10

We insist that reality is more than that, but in trying to prove it, we follow always the same process of dissolution. Can we find an answer if we just zoom in a bit further?

Gen neg 3 05

Finally, there is the Baron’s funeral, the cheapest available.

…but still, as he stood behind the coffin, about to commence the service, he felt the cold sinking into him, what should he do now, he reflected, while — his head lowered — he recited Psalm 119 to himself, should he go back for another layer,…

Gen 2

Euclid’s Game

One of the most fundamental algorithms in mathematics is the Euclidean Algorithm to compute (among other things) the greatest common divisor of two numbers.

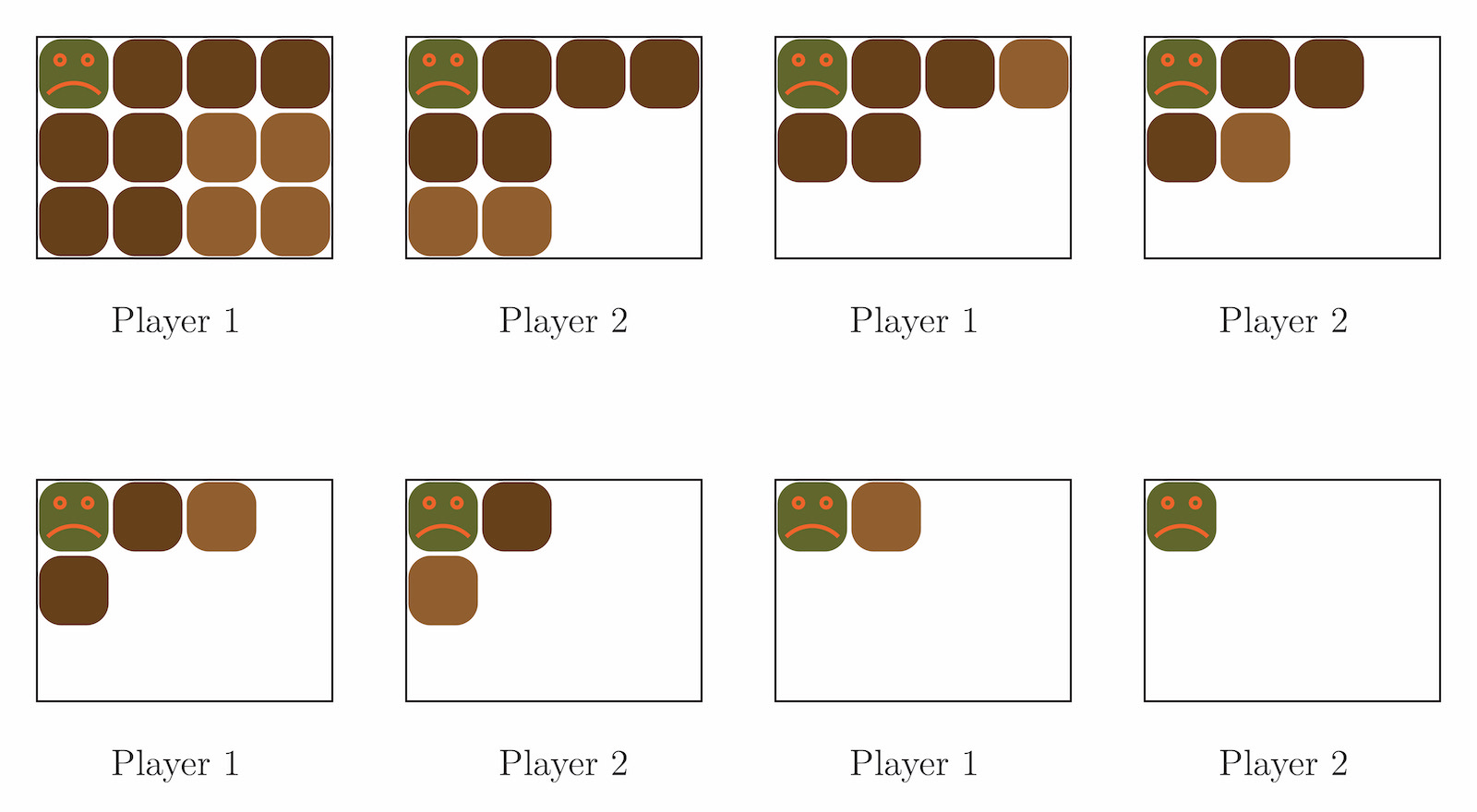
Euclid’s Game is a two person strategy game, invented by Cole and Davie in 1969, employing this algorithm, and, maybe not surprisingly, connected to the Golden Ratio. It is played with a pair of positive integers, like (11,27). A move consists of taking away from one number a non-zero multiple of the other number, so that the result is still non-negative.

So from (11,27), we can move to either (11,16) or to (11,5).
The players take turns until one number becomes zero, so that the other player is out of moves and has lost.

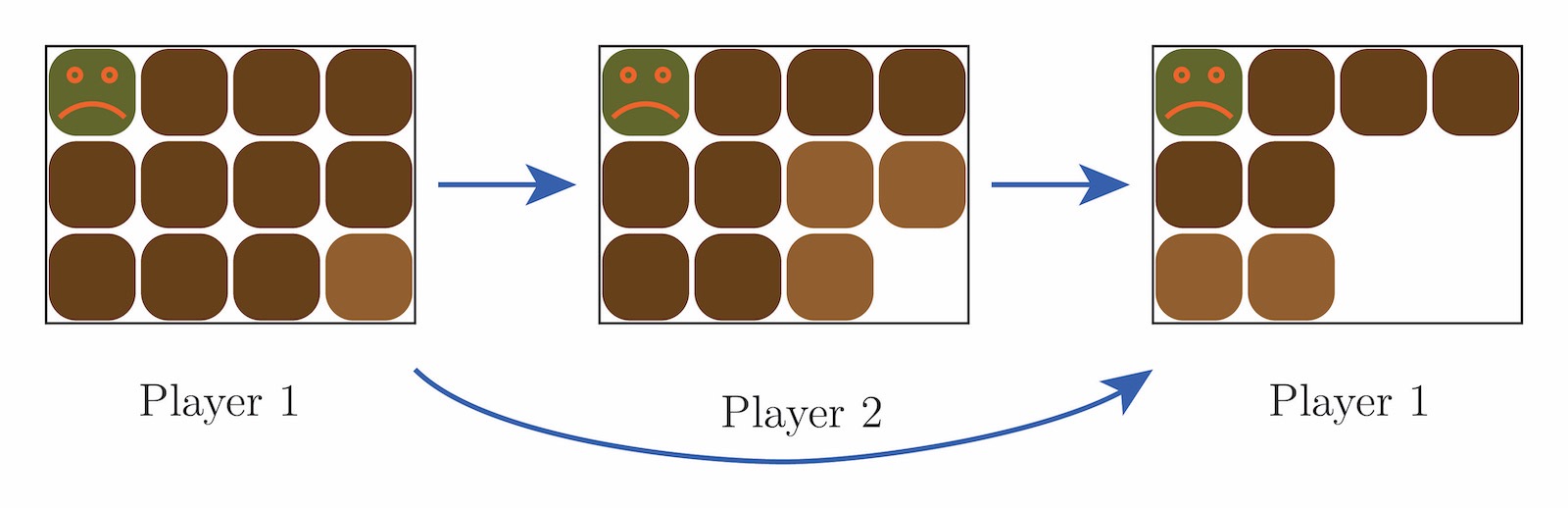
Here is a complete sample game:

(11,27)➔(11,5)➔(1,5)➔(1,3)➔(1,0)

Below is a way to visualize the possible moves by placing a blue pair (a,b) in a coordinate grid. If a<b, the possible yellow moves are obtained by decreasing the x-coordinate by a, until we get below the x-axis.

Euclid2 moves

We would like to find out when the first player has a winning strategy.

Here is a simple case: If one number is a multiple of the other, the first player can reduce the larger number to 0 and win in a single move. In particular, all pairs (a,a) are a win for the first player. By symmetry, we can from now on restrict our attention to the case that a<b.

How many different moves are possible for the pair (a,b)? We can list the moves (using the floor notation [x] for the largest integer less than or equal to x) as

(a,b-a), (a,b-2a), … , (a,b-[b/a] a),

so there are [b/a] possible moves. You can check this in the diagram above, too.

In many games, it is a good strategy to force the other player’s moves, and this turns out to be the case here as well. The first player should try to reach a pair (a’,b’) with 1< b’/ a’ <2, so that the second player has only one move left.

We will now prove:

Theorem: The first player has a winning strategy if and only if b/a is an integer, or b/a>𝜑, where 𝜑=(√5+1/2) ≈ 1.6180<2 is the Golden Ratio.
In the first case, the player wins by making the larger number 0, in the second case by moving to a position (a’,b’) where 1<b’/a'<2.

Below is a diagram showing all winning pairs (a,b) for the first player with a,b<30 in green.

Euclid2 30

We first pin down the role of the Golden Ratio.

Lemma: If 1<b/a<𝜑, there is only one move from (a,b), namely to (a’,b’)=(b-a,a), and we have b’/a’>𝜑.

Proof:
We have

$Frac a b = frac$
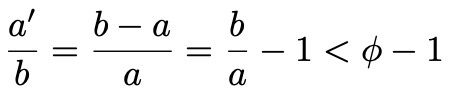
so that

$frac_b'_a'_>_fra.jpeg$
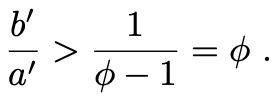
In other words, if we can move the other player into the region 1<b/a<𝜑, they are forced to move us back into the claimed winning region b’/a’ >𝜑.

The next lemma tells us when that is possible:

Lemma: Let k be a positive integer.
If k<𝜑+k-1<b/a<k+1, we can move to (a’,b’) = (b-k a, a), and this pair satisfies 1<b’/a'<𝜑. In other words, we subtract the largest amount we are allowed to.

Proof:
We have
$Phi 1< frac a b$
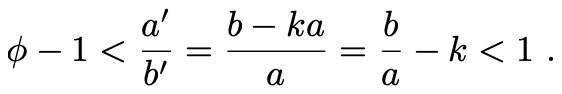
Taking reciprocals proves the claim.

We will now take care of the remaining possible ratios. Here, we take away one times less than would be allowed:

Lemma: Let k be a positive integer.
If k+1<b/a<𝜑+k, we can move to (a’,b’) = (a, b-k a). From there, only one move is possible, namely to (a”,b”) = (b-(k+1)a, a), and this pair satisfies b”/a”>𝜑.

Proof:
That the chosen move to (a, b-k a) is valid is clear, because the assumptions imply that a<b-ka. Moreover,

$frac_b'_a'_=_fra-1.jpeg$
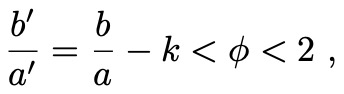
so there is only one move possible, namely to (a”,b”) = (b-(k+1)a, a). Now we have

$frac_a''_b''_=_f.jpeg$
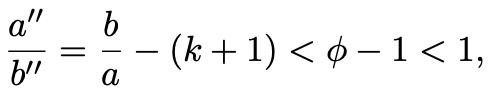
which proves that a”<b” and that b”/a”>𝜑.

The proof of the theorem now follows by combining the three lemmas.

Euclid3 20b

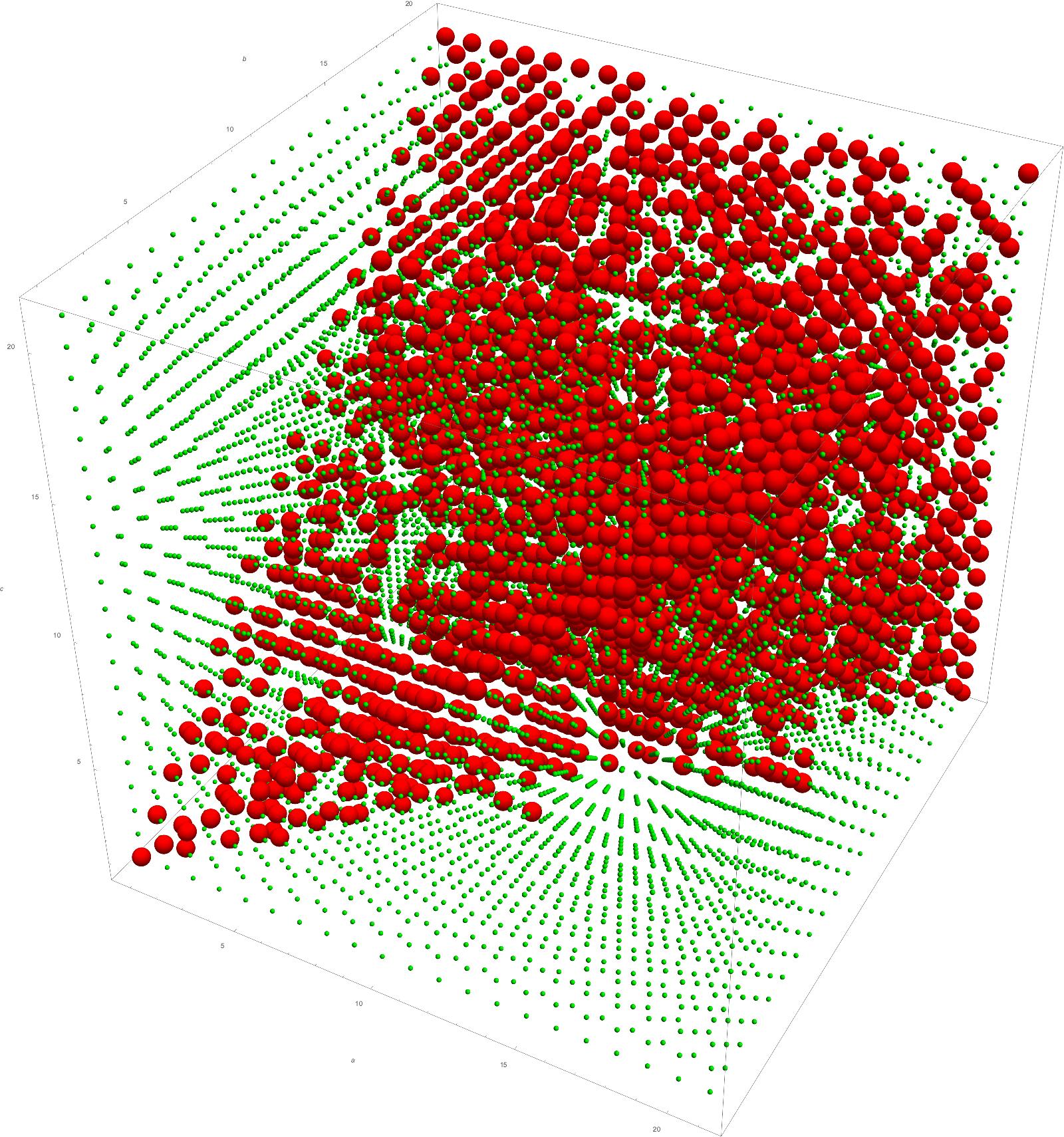
Life gets more complicated in three dimensions. One can play this game also with triples, allowing to subtract multiples of one number from either of the other two. Above is the set of winning triples in the first octant, marked with small green dots, while the losing positions are big and red. One can see they form a tetrahedral cone, but the cone is not solid, meaning that it probably won’t be as easy to find a simple winning strategy. As an impartial game, Euclid is equivalent to the game of of Nim in any dimension, it’s just not so clear, what the size of the Nim pile is.