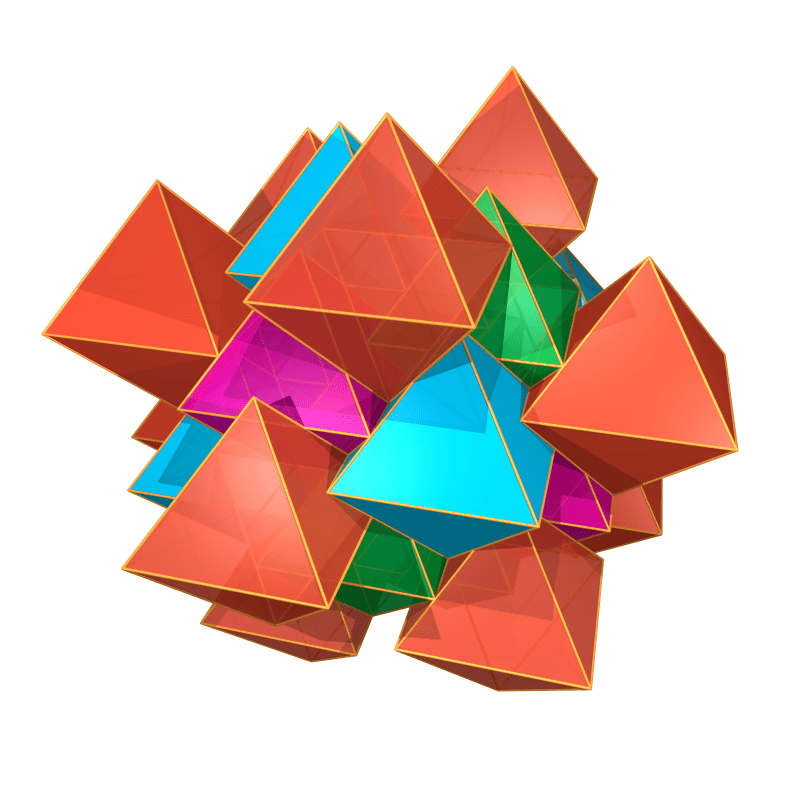Mathematics – Page 20 – The Inner Frame

Polyhedra at an Exhibition

When in 1873 Victor Hartmann died, Modest Mussorgsky visited a memorial exhibition with his friend’s drawings. Deeply impressed, he wrote a suite for piano – Pictures at an Exhibition.
The Pictures are lost, but the music survived.

Around 1910, Wassili Kandinski painted the first abstract painting. Instead of depicting recognizable things from nature, he painted abstract shapes. He even developed a theory how emotions should relate to abstract colors and shapes.

This brought the visual arts closer to music, and it is maybe not a big surprise that Kandinsky ‘composed’ a ballet for abstract shapes, to be performed to Mussorgsky’s Pictures at an Exhibition.
Kandinsky’s ballet is lost, but the idea survived.

In the spring semester 2003, I taught the class Exploring Mathematical Ideas to undergraduates majors and minors at Indiana University in Bloomington, with the idea to recreate a modern version of the ballet, using computer graphics.

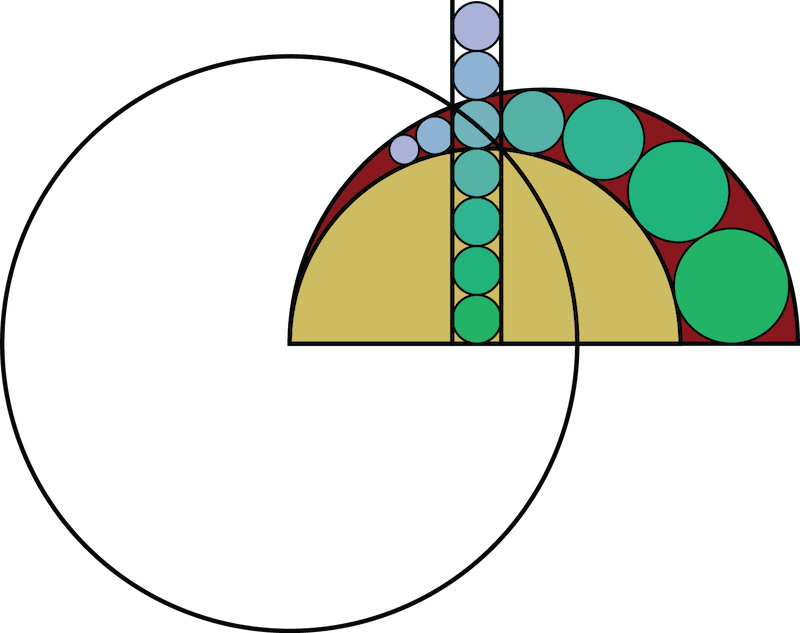
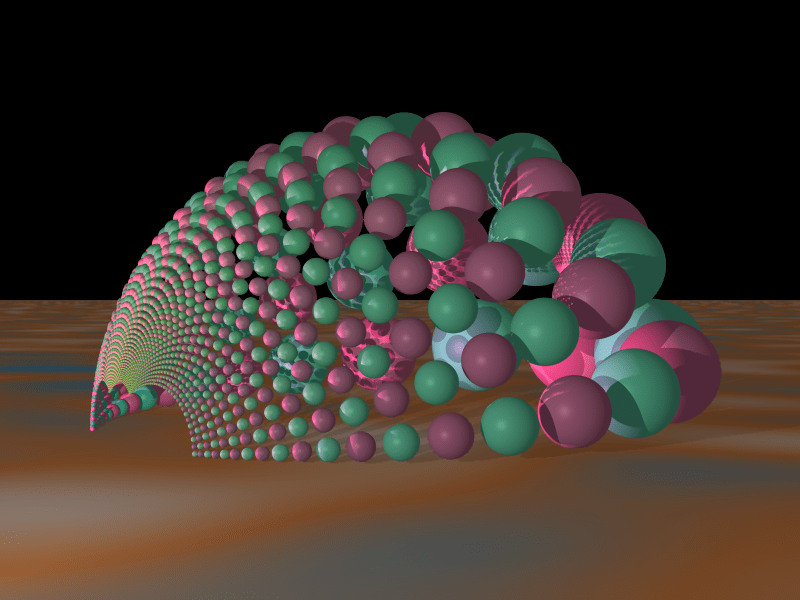
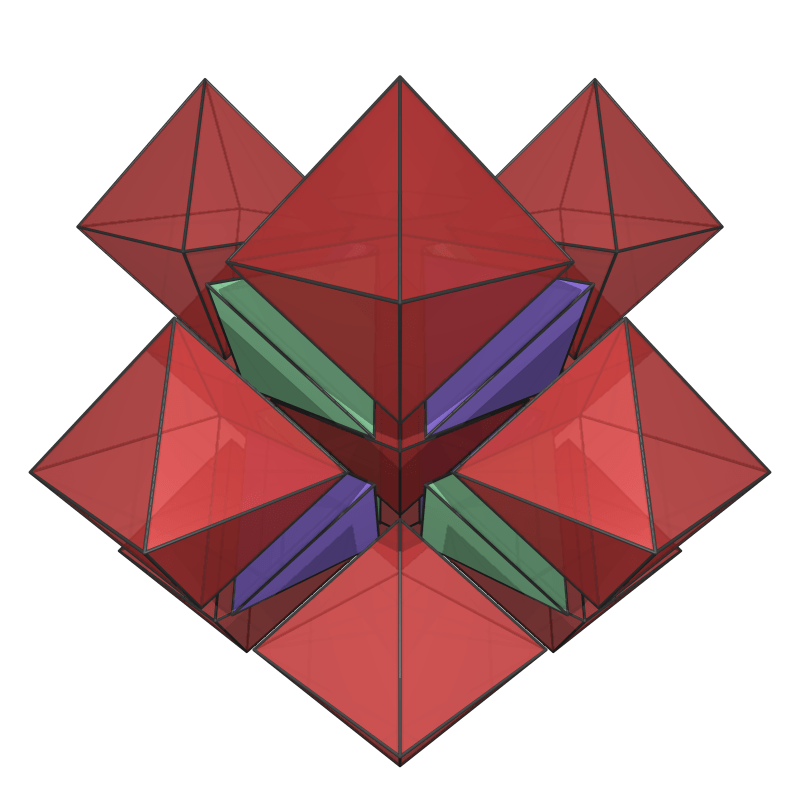
I introduced polyhedra in class early on, and used the raytracer PoVRay as an illustrational tool.

The students had to learn the basics of raytracing with PoVRay in the first half of the class.

Then we assigned one piece of the music to each student, picked a few polyhedra, created 3D models (in PoVRay), designed a few scenes, and rendered keyframes.

Then we turned to animations: What was a constant (a color, the coordinate of a point, the size of an object) could now suddenly depend on a time parameter.

This proves the concept of a variable instantly useful, and shows that being able to write down formulas for functions allows to control these geometric quantities according to the design of the scene.

How did we synchronize? The answer is: We didn’t. I didn’t ask my students to synch the movie to the music. In fact, it is usually easier to synch the music to the movie by employing a live player, than the other way round. Some of the students tried it nevertheless and succeeded amazingly well.

With some more effort, one would be able to use parameters of the music (like sound amplitude) as an input for the raytracer parameters, but our project was a zero budget project, and we didn’t have the technology.

In particular, this would require the ability to precisely align the video track with the sound track. Our (free) software did not even generate the video tracks to the correct duration…

So, instead the goal was to catch the mood of the scene, and I believe this was quite successful.

How to overcome copyrights? Using Mussorgsky’s music from commercial production so that you can publicly show the movie and distribute it is next to impossible. While Mussorgsky’s piano score is in the public domain, neither the various orchestrations are, nor are any recordings.

I was lucky to find a freely downloadable version of the orchestration by Carl Simpson, recorded by the Ithaca Symphony Orchestra under Hrant Cooper. They all and the publisher gave us permission to use the music for this class, and to show the movie. This was an interesting exercise in copyright law!

That the images on this page are so small has a reason: After a hard drive crash, the sources for the movie scenes were lost. What survives, are these images, and a low quality version of the entire 35 minute movie.

Pappus Chains (Spheres VI)

Given two circles that touch at a point, fill the gap with a chain of touching circles. This is called a Pappus chain. In the image below, I show only two semicircles, and begin the Pappus chain with a circle touching the common diameter.

Pappus chain

Now take a circle with center at the point where the two given circles touch, and perpendicular to one of the circles of the Pappus chain we pick out. The inversion at this new circle takes the two given circles to two vertical lines, and the Pappus chain to a chain of circles between these two lines. The picked circle remains fixed. Below the selected circle from the Pappus chain there are precisely as many circles as to the right of the selected circle in the Pappus chain (four in the figure). Thus the height of the selected circle is determined by its diameter and its position in the Pappus chain. That, of course, will only excite the mathematician.

The same construction works in three dimensions. Take an arrangement of spheres between two vertical half planes, and invert them at a half sphere as shown.

Prevert

The result is an arrangement of spheres between two hemispheres that touch at a point (where the spheres get really small).

Pappus out

I thought this might be an interesting way to fill a dome. Standing in front of the entrance, with reflective spheres and reflective floor, might look like this:

Appolonius small

The Beauty of the Useless

Our perceived world is 3-dimensional, but even though most of us have a decently functioning stereoscopic vision, our ability to grasp the possibilities that space has to offer are quite limited. We rule space using box shaped blocks (houses). This is convenient, because it is simple and makes space accessible even computationally.

We surround ourselves with endless repetitions of familiar shapes, largely ignorant of the fact that there are many other simple ways to create and explore rather exotic shapes with an alien but compelling esthetics.

0 2 3 x2

The images from this page are all produced using quite simple formulas, using what are called harmonic functions.
They are related to minimal surfaces (soap films), but much more flexible.

0 1 6 + 0 1 2

For the mathematician, the challenge is to find out how the algebraic properties of the formula are related to the geometric properties of the corresponding shape. This is largely done by experiment, to the surprise of many who don’t think Mathematics is an experimental science.

1 2 4 x2

At our fingertips we have infinite uncharted worlds to explore. We do not slaughter the natives, nor do we spend billions on super colliders or space probes.

Helicoidal13

Our discoveries are always fundamental, and useful only as a byproduct.

Helicoidal20

This sounds arrogant. In reality, it is just the belief that truly useful things have to be simple. This is our justification to explore simplicity for its own sake.

Mathematica2

Simple Beginnings (Spheres V)

The simplest way to arrange spheres in space is to use the cubical lattice. This is the obvious generalization of the checkerboard, and it lends itself naturally to a coloring with two colors such that neighboring spheres are differently colored. While this is not the densest sphere packing, it will be pretty dark inside.

Lattice

Leaving out the spheres of one color, painting the rest with most of RGB color space creates the following arrangement of spheres, and makes enough room for light to get through.

Lattice2

Now imagine yourself inside of it, and all spheres being reflective in addition to being colored. The formerly simplistic object becomes a dazzling fractal-like maze.

Cube small

The original bicolored sphere packing is related to a packing of space by octahedra (one for each orange sphere).
Two octahedra share then at most an edge, and the gaps can be filled with regular tetrahedra of the same edge length.

Octatetra

Minkowski discovered that octahedra can be packed much more densely. The gaps can still be filled with regular tetrahedra, but their edge length is only one third of the edge length of the octahedra.

Minkowski

Expanding Your Mind (Spheres IV)

Circles can also intersect perpendicularly in a more complicated way than discussed in Spheres IV. Like so:

Circles1

This might look complicated, but is in fact just a transformed version of the easier to grasp dart disk:

Circles0

To see how these two images are related, pretend the radial lines in the second image are in fact huge circles that all intersect in the center point. Then they will also intersect in another point, which is, in the case of lines, the ominous point at infinity, but, in the case of circles, becomes just another point in the plane. This other point and the origin are the common points of one family of circles, as you can see in the first image, and the second family of circles intersects the first perpendicularly. The first image can be transformed into the second by what is called an inversion.

If we want to repeat this in three dimensions, it is maybe best to start with the second image, replacing the radial lines by vertical green planes, and the circles by concentric blue spheres. Then, something curious happens. Lines and circles are in some sense the same thing, and so are planes and spheres. But if we look for a third family of surfaces that intersect the planes and spheres orthogonally, we need to step outside the plane/sphere paradigm. It turns out that we need vertical red cones to cut both the blue spheres and the green planes perpendicularly:

Cone

Now, coming back to the 3D version of the first image, we just need to invert the above cones, planes, spheres as to become this:

Dupin

The red surface is called a cyclide. It has two cusps that correspond to the tip of the cone and the (still ominous) point at infinity.

Now imagine that you are inside that cyclide, looking around…

Dupin2

Intelligent Design

Intelligent Design is the slightly provocative title of a small, overpriced book I wrote, containing black and white graphics that show simple geometric phenomena, with explanations.

Cassini

The constraint for the design was that it had to be cut out by a die cutter. I had acquired a Silhouette Cameo which can import AutoCAD dxf files and cut these very accurately (from card stock, for instance). One can then use these cutouts as window art.

Pursuit

The process puts interesting constraints on the graphics. It needs to be connected (otherwise it will just fall apart), simple, and simultaneously intricate.

Trapez

Under these constraints, one can still achieve a modest 3D effect by thickening parts that should be close to the viewer.

74knot

This is a 7-4 torus knot. Look at it from some distance.

The 600-Cell (Spheres III)

Various arrangements of touching spheres, with a fair amount of color, reflections, and light, can lead to startling views, like this one:

600cellbsmall

So, what are we seeing here? In short, this is the stereographic image of the 600 cell, with its vertices being represented by spheres so large that they touch in the 3-dimensional sphere.

As usual, an analogy helps. Let’s start with the ordinary cube in space. This appears to be a 3-dimensional object. We can also think of it as a tiling of the 2-dimensional sphere by spherical squares, of which one fell off here:

Cubespherical

Now, still working in the 2-sphere, place a spherical disk at each vertex of the cube with a radius so large that all the disks just touch:

Cubecaps

To view this in the plane instead of in the 2-sphere, we can apply a stereographic projection, and get a rather boring looking collection of eight touching disks.

Octapack2

Now we repeat the same procedure in one dimension higher. The cube is one of the five platonic solids in 3-space. In 4-space, there are six regular polytopes, and one of them is the 600-cell. It consist of 600 tetrahedra that we can use to tile the 3-sphere. It also has 120 vertices. Placing a small 2-sphere at each vertex and connecting adjacent vertices by thin tori in the 3-sphere, results (after stereographic projection) in the following model.

600cellc

Now make the 120 spheres so large that they just touch. The first image shows a partial view of these spheres. The spheres are all reflective, and we are standing inside the 600 cell, so we see mostly reflections of (reflections of) spheres.

Hermetic Geometry (Spheres II)

Objects in space can be either separate, intersecting, or touching. Spheres always intersect in circles, and the most fundamental case is when the angle of intersection is 90º.

Colorcircles

Let’s look at intersecting circles first. Somewhat surprisingly, two circles that meet at one point at a right angle also meet at the other intersection point at a right angle. This observation allows to construct two families of circles such that any two circles from both families meet at right angles. The first family consists of all circles that touch the x-axis at the origin, and the second family consist of all circles that touch the y-axis at the origin.

For what’s to come, let’s also look at these circles just in the first quadrant.

Halfcircles

The same procedure works in space with now three families of spheres. Each family consist of all those spheres that touch one of the coordinate planes at the origin. Viewing these in the first octant only and head-on, i.e. in the direction of the main space diagonal, shows patterns that disguise their origin quite well.

Triply1

Again, like in Spheres I, the alienation becomes extreme when we pretend that the objects are part of some large piece of architecture. The walls of the facade show the same pattern as the intersecting circles.

Triply2small

This way geometry becomes hermetic. Instead of explaining a theorem, the statement is disguised in pure appearance.

Bryce 3D (An Epitaph)

In 1997, the software department of our local book store sold heavily discounted copies of the Raytracing program Bryce,
because they had accidentally ordered Mac versions and were selling only Windows software. I purchased a copy, not knowing what this
would get me into.

Catalan

I had been making images of minimal surfaces the past year with Mathematica, and the 3D graphics of Mathematica could be first exported into Autocad DXF files, and then imported into Bryce.

Chm

Bryce is primarily a landscape renderer. The tools let you create terrains, and it comes with a sophisticated texture editor that lets you literally compose all kinds of textures for your objects.

Having abstract mathematical shapes in (somewhat) familiar landscapes seems to stretch our minds just right.

In 1997, computers were slow. Most images had to be rendered over night, to get screen filling sizes. And these were screens from 1997, too.

Tortor

The user interface of Bryce (by Kai Krause and Eric Wenger) was revolutionary, and still leaves not much to be desired today. In 1999, Bryce reached its high point with a a vastly improved texture editor. Then the decline began. Fist, it was sold to Corel, and then to DAZ 3D.

Riemann

The current version is Bryce 7, and does not work with recent Mac OS X versions. In runs under OS X.6, but is quite unstable, preventing me to rerender the old files to proper sizes.

Blackhandle
This has been a lot of fun.

Reflections (Spheres I)

Large scale mirrors like the surface of a lake are awe inspiring. They simultaneously create complexity and
order. The order comes from the inherent symmetry, and the complexity from subtle differences between original and
mirror image.

Things get considerably more complicated when the mirrors are curved. The Cloud Gate sculpture by Anish Kapoor (the Bean) in the Millennium Park in Chicago is a popular example. The multiple reflections create an immediately surprising chaotic richness of the reflection: Taking one step to the side changes the appearance of the reflection dramatically. But the sculpture also extends and therefore enriches the architecture.

DSC 6142

Motivated by this, I began to experiment with the spherical mirrors, spheres being the simplest curved shapes.
For multiple spheres touching each other there is a surprising phenomenon that is best understood when we begin with seven spheres of equal size, one at the center, and the remaining six surrounding the central sphere symmetrically. Complete this configuration by adding two planes that touch all seven spheres. Now pretend that the two planes are in fact also gigantic spheres. Than these two and the central sphere all touch the remaining six spheres, which in turn form a chain where consecutive spheres touch.

Soddysimple

It turns out that this picture is not just an approximation that only works in the ideal situation shown above where the big spheres are planes, but in fact works for spheres of any size. This is the content of Soddy’s theorem.

Soddy2

To turn this into some sort of virtual sculpture, it is best to make just one of the spheres a plane. Then place two spheres onto the plane so that they touch. If you continue placing more spheres onto the plane so that they also touch the two initial spheres and the previously placed sphere, they will form a chain of six spheres of which the last again touches the first.

Soddy0

Now imagine these being really large, reflective, slightly translucent, and illuminated with colored light sources. You might see something like this:

Soddy

This is the first of a series of images featuring ray traced spheres.